Hackerrank Absolute Permutation Solution

.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%} .MathJax_SVG .MJX-monospace {font-family: monospace} .MathJax_SVG .MJX-sans-serif {font-family: sans-serif} .MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0} .MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none} .mjx-svg-href {fill: blue; stroke: blue} .MathJax_SVG_LineBox {display: table!important} .MathJax_SVG_LineBox span {display: table-cell!important; width: 10000em!important; min-width: 0; max-width: none; padding: 0; border: 0; margin: 0}
We define to be a permutation of the first natural numbers in the range . Let denote the value at position in permutation using -based indexing.
is considered to be an absolute permutation if holds true for every .
Given and , print the lexicographically smallest absolute permutation . If no absolute permutation exists, print -1.
For example, let giving us an array . If we use based indexing, create a permutation where every . If , we could rearrange them to : pos[i] i |Difference|3 1 24 2 21 3 22 4 2
Function Description
Complete the absolutePermutation function in the editor below. It should return an integer that represents the smallest lexicographically smallest permutation, or if there is none.
absolutePermutation has the following parameter(s):
- n: the upper bound of natural numbers to consider, inclusive
- k: the integer difference between each element and its index
Input Format.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%} .MathJax_SVG .MJX-monospace {font-family: monospace} .MathJax_SVG .MJX-sans-serif {font-family: sans-serif} .MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0} .MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none} .mjx-svg-href {fill: blue; stroke: blue} .MathJax_SVG_LineBox {display: table!important} .MathJax_SVG_LineBox span {display: table-cell!important; width: 10000em!important; min-width: 0; max-width: none; padding: 0; border: 0; margin: 0}
The first line contains an integer , the number of test cases.
Each of the next lines contains space-separated integers, and .
Constraints.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%} .MathJax_SVG .MJX-monospace {font-family: monospace} .MathJax_SVG .MJX-sans-serif {font-family: sans-serif} .MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0} .MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none} .mjx-svg-href {fill: blue; stroke: blue} .MathJax_SVG_LineBox {display: table!important} .MathJax_SVG_LineBox span {display: table-cell!important; width: 10000em!important; min-width: 0; max-width: none; padding: 0; border: 0; margin: 0}
Output Format.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%} .MathJax_SVG .MJX-monospace {font-family: monospace} .MathJax_SVG .MJX-sans-serif {font-family: sans-serif} .MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0} .MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none} .mjx-svg-href {fill: blue; stroke: blue} .MathJax_SVG_LineBox {display: table!important} .MathJax_SVG_LineBox span {display: table-cell!important; width: 10000em!important; min-width: 0; max-width: none; padding: 0; border: 0; margin: 0}
On a new line for each test case, print the lexicographically smallest absolute permutation. If no absolute permutation exists, print -1.
Sample Input.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%} .MathJax_SVG .MJX-monospace {font-family: monospace} .MathJax_SVG .MJX-sans-serif {font-family: sans-serif} .MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0} .MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none} .mjx-svg-href {fill: blue; stroke: blue}
3
2 1
3 0
3 2
Sample Output.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%} .MathJax_SVG .MJX-monospace {font-family: monospace} .MathJax_SVG .MJX-sans-serif {font-family: sans-serif} .MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0} .MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none} .mjx-svg-href {fill: blue; stroke: blue}
2 1
1 2 3
-1
Explanation.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%} .MathJax_SVG .MJX-monospace {font-family: monospace} .MathJax_SVG .MJX-sans-serif {font-family: sans-serif} .MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0} .MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none} .mjx-svg-href {fill: blue; stroke: blue}
Test Case 0:
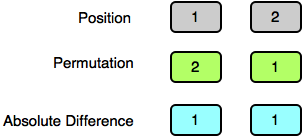
Test Case 1:
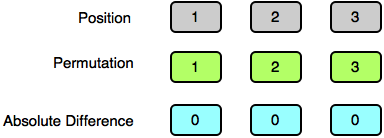
Test Case 2:
No absolute permutation exists, so we print -1 on a new line.
Solution in java8
Approach 1.
import java.io.*;
import java.math.*;
import java.security.*;
import java.text.*;
import java.util.*;
import java.util.concurrent.*;
import java.util.regex.*;
public class Solution {
// Complete the absolutePermutation function below.
static int[] absolutePermutation(int n, int k) {
int[] per = new int[n];
int d = 1;
for (int i = 0, j = 0; i < n; i++, j++) {
if (j == k) {
d *= -1;
j = 0;
}
int value = i + 1 + k * d;
if (value < 1 || value > n)
return new int[]{-1};
per[i] = value;
}
return per;
}
private static final Scanner scanner = new Scanner(System.in);
public static void main(String[] args) throws IOException {
BufferedWriter bufferedWriter = new BufferedWriter(new FileWriter(System.getenv("OUTPUT_PATH")));
int t = scanner.nextInt();
scanner.skip("(\r\n|[\n\r\u2028\u2029\u0085])?");
for (int tItr = 0; tItr < t; tItr++) {
String[] nk = scanner.nextLine().split(" ");
int n = Integer.parseInt(nk[0]);
int k = Integer.parseInt(nk[1]);
int[] result = absolutePermutation(n, k);
for (int i = 0; i < result.length; i++) {
bufferedWriter.write(String.valueOf(result[i]));
if (i != result.length - 1) {
bufferedWriter.write(" ");
}
}
bufferedWriter.newLine();
}
bufferedWriter.close();
scanner.close();
}
}
Approach 2.
import java.io.*;
import java.math.*;
import java.security.*;
import java.text.*;
import java.util.*;
import java.util.concurrent.*;
import java.util.regex.*;
public class Solution {
// Complete the absolutePermutation function below.
static int[] absolutePermutation(int n, int k) {
int[] per = new int[n];
int d = 1;
for (int i = 0, j = 0; i < n; i++, j++) {
if (j == k) {
d *= -1;
j = 0;
}
int value = i + 1 + k * d;
if (value < 1 || value > n)
return new int[]{-1};
per[i] = value;
}
return per;
}
private static final Scanner scanner = new Scanner(System.in);
public static void main(String[] args) throws IOException {
BufferedWriter bufferedWriter = new BufferedWriter(new FileWriter(System.getenv("OUTPUT_PATH")));
int t = scanner.nextInt();
scanner.skip("(\r\n|[\n\r\u2028\u2029\u0085])?");
for (int tItr = 0; tItr < t; tItr++) {
String[] nk = scanner.nextLine().split(" ");
int n = Integer.parseInt(nk[0]);
int k = Integer.parseInt(nk[1]);
int[] result = absolutePermutation(n, k);
for (int i = 0; i < result.length; i++) {
bufferedWriter.write(String.valueOf(result[i]));
if (i != result.length - 1) {
bufferedWriter.write(" ");
}
}
bufferedWriter.newLine();
}
bufferedWriter.close();
scanner.close();
}
}
Approach 3.
import java.io.*;
import java.math.*;
import java.security.*;
import java.text.*;
import java.util.*;
import java.util.concurrent.*;
import java.util.regex.*;
import java.util.stream.*;
public class Solution {
// Complete the absolutePermutation function below.
static int[] absolutePermutation(int n, int k) {
int[] noPerm = { -1 };
int[] pool = IntStream.range(1, (n+1)).toArray();
if (k == 0) return pool;
int[] perm = new int[n];
int prosimo = 1;
for (int i=1; i<=n; i++) {
perm[i-1] = pool[i-1] + (prosimo * k);
if (perm[i-1] > n) {
return noPerm;
} else if (i % k == 0) {
prosimo *= -1;
}
}
return perm;
}
private static final Scanner scanner = new Scanner(System.in);
public static void main(String[] args) throws IOException {
BufferedWriter bufferedWriter = new BufferedWriter(new FileWriter(System.getenv("OUTPUT_PATH")));
int t = scanner.nextInt();
scanner.skip("(\r\n|[\n\r\u2028\u2029\u0085])?");
for (int tItr = 0; tItr < t; tItr++) {
String[] nk = scanner.nextLine().split(" ");
int n = Integer.parseInt(nk[0]);
int k = Integer.parseInt(nk[1]);
int[] result = absolutePermutation(n, k);
for (int i = 0; i < result.length; i++) {
bufferedWriter.write(String.valueOf(result[i]));
if (i != result.length - 1) {
bufferedWriter.write(" ");
}
}
bufferedWriter.newLine();
}
bufferedWriter.close();
scanner.close();
}
}
Solution in python3
Approach 1.
#!/bin/python3
import os
def absolutePermutation(n, k):
if k == 0:
return range(1, n + 1)
if n % (2 * k):
return [-1]
result = [(i - k + 1) if (i % (2 * k)) >= k else (i + k + 1) for i in range(n)]
return result
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
for t_itr in range(int(input())):
n, k = map(int, input().strip().split())
result = absolutePermutation(n, k)
fptr.write(' '.join(map(str, result)))
fptr.write('\n')
fptr.close()
Approach 2.
# Only the case when k!=0 and n % (2*k) == 0
def absolutePermutation(n,k):
num_segments = n // (2*k)
base_1 = [i for i in range(1, k+1)]
base_2 = [i+k for i in range(1, k+1)]
base = base_2 + base_1
ans = base
for i in range(1, num_segments):
next_1 = [b + 2*k*i for b in base_1]
next_2 = [b + 2 * k * i for b in base_2]
next = next_2 + next_1
ans.extend(next)
return ans
t = int(input())
for t_itr in range(t):
nk = input().split()
n = int(nk[0])
k = int(nk[1])
if k == 0:
ans = list(range(1, n + 1))
print(*ans)
elif n % (2*k) != 0:
print(-1)
else:
result = absolutePermutation(n, k)
print(*result)
Approach 3.
#!/bin/python3
import math
import os
import random
import re
import sys
# Complete the absolutePermutation function below.
def absolutePermutation(n, k):
P=[i for i in range(1,n+1)]
if k==0: return P
if n%2==1: return [-1]
if n%k!=0 or (n//k)%2!=0: return [-1]
for i in range(0,(n//k)//2):
j=i*k*2
temp=P[j:j+k]
P[j:j+k]=P[j+k:j+2*k]
P[j+k:j+2*k]=temp
return P
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input())
for t_itr in range(t):
nk = input().split()
n = int(nk[0])
k = int(nk[1])
result = absolutePermutation(n, k)
fptr.write(' '.join(map(str, result)))
fptr.write('\n')
fptr.close()
Solution in cpp
Approach 1.
#include <map>
#include <set>
#include <list>
#include <cmath>
#include <ctime>
#include <deque>
#include <queue>
#include <stack>
#include <string>
#include <bitset>
#include <cstdio>
#include <limits>
#include <vector>
#include <climits>
#include <cstring>
#include <cstdlib>
#include <fstream>
#include <numeric>
#include <sstream>
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
int main(){
int t;
cin >> t;
for(int a0 = 0; a0 < t; a0++){
int N;
int K;
cin >> N >> K;
if(K == 0){
for(int i=1; i<N; i++) cout<<i <<" ";
cout<< N <<endl;
continue;
}
if((N/K)%2 != 0 || N%K != 0){
cout<<-1 <<endl;
continue;
}
int flag = 0;
for(int i=1; i<N; i++){
cout<< ((flag%2 == 0)? i+K: i-K) <<" ";
if(i%K == 0) flag++;
}
cout<<(N-K) <<endl;
}
return 0;
}
Approach 2.
#include <map>
#include <set>
#include <list>
#include <cmath>
#include <ctime>
#include <deque>
#include <queue>
#include <stack>
#include <string>
#include <bitset>
#include <cstdio>
#include <limits>
#include <vector>
#include <climits>
#include <cstring>
#include <cstdlib>
#include <fstream>
#include <numeric>
#include <sstream>
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
int main(){
int t;
cin >> t;
for(int a0 = 0; a0 < t; a0++){
int n;
int k;
cin >> n >> k;
if (k !=0 && (n % k) > 0)
cout << -1;
else {
bool doAdd = (k != 0); // first value has to be later in the array
for (int i = 1; i <= n; ++i) {
if (i > 1) cout << " ";
if (!doAdd)
cout << i - k;
else {
cout << i + k;
}
if (k != 0 && i%k==0)
doAdd = !doAdd;
}
}
cout << endl;
}
return 0;
}
Approach 3.
#include <map>
#include <set>
#include <list>
#include <cmath>
#include <ctime>
#include <deque>
#include <queue>
#include <stack>
#include <string>
#include <bitset>
#include <cstdio>
#include <limits>
#include <vector>
#include <climits>
#include <cstring>
#include <cstdlib>
#include <fstream>
#include <numeric>
#include <sstream>
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
int main(){
int t;
cin >> t;
for(int a0 = 0; a0 < t; a0++){
int n;
int k;
cin >> n >> k;
if(k==0)
{
for(int i=1;i<=n;i++)
{
cout<<i<<" ";
}cout<<endl;
continue;
}
vector<int> a(n+1);
if((n%k)==0)
{
for(int i=0;i<n;i++)
{
if((i/k)%2==0)
{
a[i]=i+k+1;
}
else{
a[i]=i-k+1;
}
}
for(int i=0;i<n;i++)
{
cout<<a[i]<<" ";
}cout<<endl;
}
else{
cout<<"-1"<<endl;
}
}
return 0;
}
