Hackerrank - Cloudy Day Solution

Quibdó in Colombia is one among the cities that receive maximum rainfall in the world.
All year round, the city is covered in clouds. The city has many towns, located on a one-dimensional line. The positions and populations of each town on the number line are known to you. Every cloud covers all towns located at a certain distance from it. A town is said to be in darkness if there exists at least one cloud such that the town is within the cloud's range. Otherwise, it is said to be sunny.

The city council has determined that they have enough money to remove exactly one cloud using their latest technology. Thus they want to remove the cloud such that the fewest number of people are left in darkness after the cloud is removed. What is the maximum number of people that will be in a sunny town after removing exactly one cloud?
Note: If a town is not covered by any clouds, then it is already considered to be sunny, and the population of this town must also be included in the final answer.
Complete the function maximumPeople which takes four arrays representing the populations of each town, locations of the towns, locations of the clouds, and the extents of coverage of the clouds respectively, and returns the maximum number of people that will be in a sunny town after removing exactly one cloud.
Input Format
The first line of input contains a single integer , the number of towns.
The next line contains space-separated integers . The integer in this line denotes the population of the town.
The next line contains space-separated integers denoting the location of the town on the one-dimensional line.
The next line consists of a single integer denoting the number of clouds covering the city.
The next line contains space-separated integers the of which denotes the location of the cloud on the coordinate axis.
The next line consists of space-separated integers denoting the range of the cloud.
Note: The range of each cloud is computed according to its location, i.e., the cloud is located at position and it covers every town within a distance of from it. In other words, the cloud covers every town with location in the range .
Constraints
Output Format
Print a single integer denoting the maximum number of people that will be in a sunny town by removing exactly one cloud.
Sample Input 0
2
10 100
5 100
1
4
1Sample Output 0
110Explanation 0
In the sample case, there is only one cloud which covers the first town. Our only choice is to remove this sole cloud which will make all towns sunny, and thus, all people will live in a sunny town.
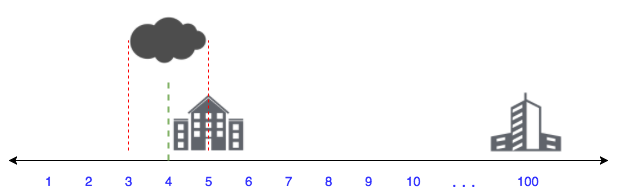
As you can see, the only cloud present, is at location on the number line and has a range , so it covers towns located at , and on the number line. Hence, the first town is covered by this cloud and removing this cloud makes all towns sunny.
Solution in Python
from collections import Counter
def getHouses(arr):
for x,y in arr.items():
yield (x,y,"H")
def getClouds(arr):
t = 0
for i in sorted(arr):
t+= arr[i]
yield (i,t,"C")
def maximumPeople(p, x, y, r):
a = Counter()
b = Counter()
c = Counter()
for i,j in zip(p,x):
a[j]+=i
for i,j in zip(y,r):
b[i-j] +=1
b[i+j+1] -=1
c[i-j] = i+j+1
houses = getHouses(a)
clouds = getClouds(b)
cloudsAbove = 0
currentCloud = -1
sunnyCity = 0
cloudyCity = Counter()
for i,j,k in sorted(list(clouds)+list(houses)):
if k == "C":
cloudsAbove = j
if currentCloud == -1 or (cloudsAbove == 1 and i>=c[currentCloud]):
currentCloud = i
elif cloudsAbove == 1:
cloudyCity[currentCloud]+=j
elif cloudsAbove == 0 :
sunnyCity+=j
return sunnyCity+max(cloudyCity.values() or [0])
n = int(input())
p = list(map(int,input().split()))
x = list(map(int,input().split()))
m = int(input())
y = list(map(int,input().split()))
r = list(map(int,input().split()))
print(maximumPeople(p, x, y, r))
