Hackerrank - Kangaroo Solution

You are choreographing a circus show with various animals. For one act, you are given two kangaroos on a number line ready to jump in the positive direction (i.e, toward positive infinity).

• The first kangaroo starts at location  and moves at a rate of  meters per jump.
• The second kangaroo starts at location  and moves at a rate of  meters per jump.

You have to figure out a way to get both kangaroos at the same location at the same time as part of the show. If it is possible, return YES, otherwise return NO.

For example, kangaroo  starts at  with a jump distance  and kangaroo  starts at  with a jump distance of . After one jump, they are both at , (, ), so our answer is YES.

Function Description

Complete the function kangaroo in the editor below. It should return YES if they reach the same position at the same time, or NO if they don't.

kangaroo has the following parameter(s):

• x1, v1: integers, starting position and jump distance for kangaroo 1
• x2, v2: integers, starting position and jump distance for kangaroo 2

Input Format

A single line of four space-separated integers denoting the respective values of , , , and .

Constraints

Output Format

Print YES if they can land on the same location at the same time; otherwise, print NO.

Note: The two kangaroos must land at the same location after making the same number of jumps.

Sample Input 0

0 2 5 3

Sample Output 0

NO

Explanation 0

The two kangaroos jump through the following sequence of locations:

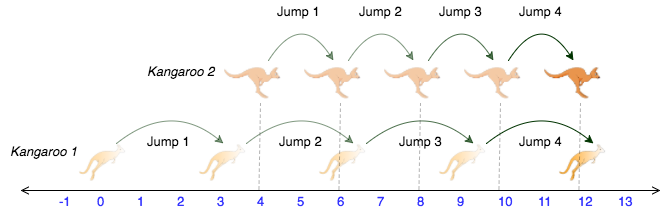
From the image, it is clear that the kangaroos meet at the same location (number  on the number line) after same number of jumps ( jumps), and we print YES.

Sample Input 1

0 3 4 2

Sample Output 1

NO

Explanation 1

The second kangaroo has a starting location that is ahead (further to the right) of the first kangaroo's starting location (i.e., ). Because the second kangaroo moves at a faster rate (meaning ) and is already ahead of the first kangaroo, the first kangaroo will never be able to catch up. Thus, we print NO.

Solution in Python

def kangaroo(x1, v1, x2, v2):
    if (v1 > v2) and (x2 - x1) % (v2 - v1) == 0:
        return "YES"
    else:
        return "NO"

x1,v1,x2,v2 = map(int,input().split())
result = kangaroo(x1, v1, x2, v2)
print(result)

Answer Explanation

Let us assume both kangaroos make y jumps.

The end position of kangaroo 1 after making y jumps will be

Initial position(k1) + Distance covered in y jumps (v1*y)

Which becomes

x1+v1*y

The end position of kangaroo 2 after making y jumps will be

x2+v2*y

For kangaroos to meet at same point. End position of both kangaroos must be equal.

x1+v1*y = x2+v2*y

Solving the above equation we get

-> x1+v1*y == x2+v2*y
-> x1-x2 == v2*y-v1*y
-> x1-x2 == (v2-v1)*y

Since x1-x2 is the product of (v2-v1) and some value y

Therefore x1-x2 must be divisible by v2-v1 for the two kangaroos to meet at same point.

(x1-x2) % (v2-v1) == 0

Another condition which needs to be satisfied is

v1>v2

It is given in the constraints, that x1<x2 which means kangaroo 1 lack behind kangaroo 2 therefore for the both kangaroos to meet at a same point. kangaroo 1 must be faster than kangaroo 2. i.e. v1>v2

Hence our final condition for 2 kangaroos to meet becomes

(x1-x2) % (v2-v1) == 0 and v1>v2

Alternative solution using while loop (Not recommended)

def kangaroo(x1, v1, x2, v2):
    if v1>v2:
        while x1<x2:
            x1+=v1
            x2+=v2
    return "YES" if x1==x2 else "NO"

x1,v1,x2,v2 = map(int,input().split())
result = kangaroo(x1, v1, x2, v2)
print(result)

Answer Explanation

Given constraints

x1<x2,

As we already know that only the faster kangaroo will be able to catch up with the slower one. So we first check which of the two kangaroo is faster.

If v1<v2, kangaroo 1 will never reach the position of kangaroo 2.

Then we keep incrementing the position of both kangaroos according to their speed, until the position of Kangaroo 1 will be greater than or equal to kangaroo 2.

If the position of kangaroo 1 becomes equal to the position of kangaroo 2 then our function will return YES else it will return NO.