HackerRank - Minimum Height Triangle solution

Given integers  and , find the smallest integer , such that there exists a triangle of height , base , having an area of at least .

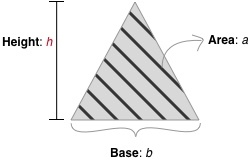
Input Format

In the first and only line, there are two space-separated integers  and , denoting respectively the base of a triangle and the desired minimum area.

Constraints

Output Format

In a single line, print a single integer , denoting the minimum height of a triangle with base  and area at least .

Sample Input 02 2

Sample Output 02

Explanation 0

The task is to find the smallest integer height of the triangle with base  and area at least . It turns out, that there are triangles with height , base  and area , for example a triangle with corners in the following points: :

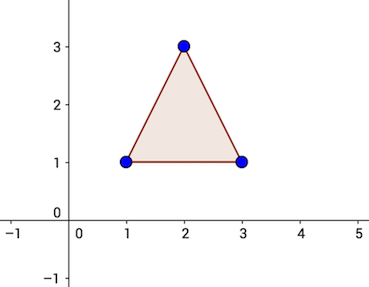
It can be proved that there is no triangle with integer height smaller than , base  and area at least .

Sample Input 117 100

Sample Output 112

Explanation 1

The task is to find the smallest integer height of the triangle with base  and area at least . It turns out, that there are triangles with height , base  and area , for example a triangle with corners in the following points: .

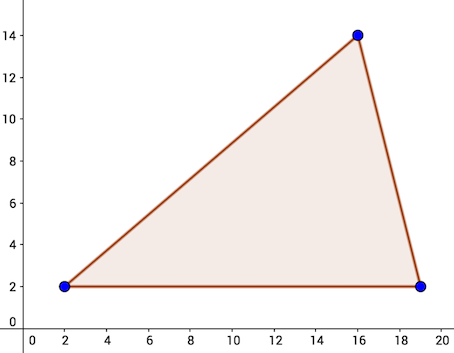
It can be proved that there is no triangle with integer height smaller than , base  and area at least .

Solution in Python

#!/bin/python3

import sys,math

def lowestTriangle(base, area):
    return math.ceil(area*2/base)

base, area = input().strip().split(' ')
base, area = [int(base), int(area)]
height = lowestTriangle(base, area)
print(height)