Hackerrank - Separate the Numbers Solution

A numeric string, , is beautiful if it can be split into a sequence of two or more positive integers, , satisfying the following conditions:

1. for any  (i.e., each element in the sequence is  more than the previous element).
2. No  contains a leading zero. For example, we can split  into the sequence , but it is not beautiful because  and  have leading zeroes.
3. The contents of the sequence cannot be rearranged. For example, we can split  into the sequence , but it is not beautiful because it breaks our first constraint (i.e., ).

The diagram below depicts some beautiful strings:

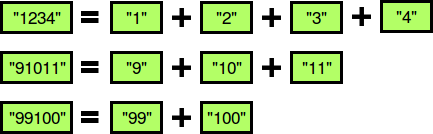
You must perform  queries where each query consists of some integer string . For each query, print whether or not the string is beautiful on a new line. If it's beautiful, print YES x, where  is the first number of the increasing sequence. If there are multiple such values of , choose the smallest. Otherwise, print NO.

Function Description

Complete the separateNumbers function in the editor below. It should print a string as described above.

separateNumbers has the following parameter:

• s: an integer value represented as a string

Input Format

The first line contains an integer , the number of strings to evaluate.
Each of the next  lines contains an integer string  to query.

Constraints

Output Format

For each query, print its answer on a new line (i.e., either YES x where  is the smallest first number of the increasing sequence, or NO).

Sample Input 0

7
1234
91011
99100
101103
010203
13
1

Sample Output 0

YES 1
YES 9
YES 99
NO
NO
NO
NO

Explanation 0

The first three numbers are beautiful (see the diagram above). The remaining numbers are not beautiful:

• For , all possible splits violate the first and/or second conditions.
• For , it starts with a zero so all possible splits violate the second condition.
• For , the only possible split is , which violates the first condition.
• For , there are no possible splits because  only has one digit.

Sample Input 1

4
99910001001
7891011
9899100
999100010001

Sample Output 1

YES 999
YES 7
YES 98
NO

Solution in Python

def sequential(s,sub_string):
    if not s: return True
    if s.startswith(sub_string):
        l = len(sub_string)
        return sequential(s[l:],str(int(sub_string)+1))
    return False
    
def separateNumbers(s):
    for i in range(1,len(s)//2+1):
        sub_string = s[:i]
        if sequential(s,sub_string):
            return "YES "+sub_string
    return "NO"

for _ in range(int(input())):
    s = input()
    print(separateNumbers(s))

First we create a recursive function, which I have named as sequential. It accepts two parameters string s and substring.

Basically what is does is check if our string starts with given substring,

Example, s = "101112"

If we take substring as "1".

First it checks if s starts with "1". If it starts with "1", we will increment our substring and "1" becomes "2".

Now using recursion we call the function itself to check if the remaining part of string that is "01112" starts with "2".

If it doesn't our function will return False.

---

If we take substring as "10".

First it checks if s starts with "10". If it starts with "10", we will increment our substring and "10" becomes "11".

Now using recursion we call the function itself to check if the remaining part of string that is "1112" starts with "11".

Since it starts with "11". We again increment our substring by 1 and it becomes "12"

Again using recursion we call the function itself to check if the remaining part of string that is "12" starts with "12".

Since it starts with "12". We again increment our substring by 1 and it becomes "13"

Again using recursion we call the function itself to check if the remaining part of string that is "" which is an empty string starts with "13".

Notice that now s = "" which is an empty string. Therefore it means we have successfully checked all part of our string and it forms a perfect sequence.

If you may have noticed, we have added the following function

if not s: return True

So when no more substring is left our function will return True

---

The seperate number function is a simple for loop which initially take the first character of our original string a substring. Then call our helper function sequential, If it returns false we will further take first two character as substring then 3 and so on, upto half of the string

Example if our string is "101112"

We will first take "1" as sub_string, then "10" , then "101".

If for any substring our sequential function returns True, we will break our loop and return "YES"

If none of our substrings returns True we will return "NO"