Hackerrank - Sock Merchant Solution

John works at a clothing store. He has a large pile of socks that he must pair by color for sale. Given an array of integers representing the color of each sock, determine how many pairs of socks with matching colors there are.
For example, there are socks with colors . There is one pair of color and one of color . There are three odd socks left, one of each color. The number of pairs is .
Function Description
Complete the sockMerchant function in the editor below. It must return an integer representing the number of matching pairs of socks that are available.
sockMerchant has the following parameter(s):
- n: the number of socks in the pile
- ar: the colors of each sock
Input Format
The first line contains an integer , the number of socks represented in .
The second line contains space-separated integers describing the colors of the socks in the pile.
Constraints
- where
Output Format
Return the total number of matching pairs of socks that John can sell.
Sample Input
9
10 20 20 10 10 30 50 10 20
Sample Output
3
Explanation
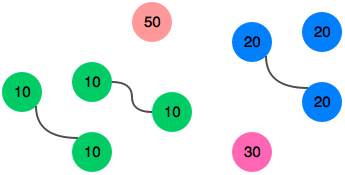
John can match three pairs of socks.
Solution in Python
from collections import Counter
def sockMerchant(n,arr):
n = Counter(arr)
return sum(i//2 for i in n.values())
n = input()
arr = list(map(int,input().split()))
print(sockMerchant(n,arr))Explanation
We first take input from user
>>> arr = list(map(int,input().split()))
>>> arr
[10, 20, 20, 10, 10, 30, 50, 10, 20]Then we use Counter to group and count all similar type of socks
>>> n = Counter(arr)
>>> n
Counter({10: 4, 20: 3, 30: 1, 50: 1})
>>> n.values()
dict_values([4, 3, 1, 1])Now we just have to loop through n.values() and divide by 2 which gives us total possible pairs
4//2 = 2
3//2 = 1
1//2 =0
1//2 =0
Total pairs = 2 + 1 + 0 +0 = 3
>> sum(i//2 for i in n.values())
3