Leetcode - Word Search Solution

Given an m x n grid of characters board and a string word, return true if word exists in the grid.

The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.

Note: There will be some test cases with a board or a word larger than constraints to test if your solution is using pruning.

Example 1:

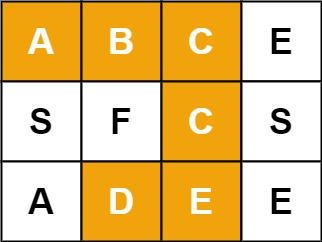
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
Output: true

Example 2:

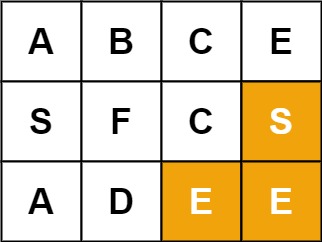
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
Output: true

Example 3:

Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
Output: false

Constraints:

• m == board.length
• n = board[i].length
• 1 <= m, n <= 6
• 1 <= word.length <= 15
• board and word consists of only lowercase and uppercase English letters.

Solution in python

class Solution(object):
  def exist(self, board, word):
      board = board
      word = word
      def ExistCharacter(i,j,index,word):
        if (i < 0 or i >= len(board) or j < 0 or j >= len(board[i])) :
            return False   

        # when index character does not match  
        if(board[i][j] != word[index])  :
            return False   

        # when completely matched  
        if(index == len(word) - 1)  :
            return True  
        # mark the current character  
        board[i][j] = '#'  

        # check every direction  
        found = ExistCharacter(i, j - 1, index + 1, word) or ExistCharacter(i, j + 1, index + 1, word) or ExistCharacter(i - 1, j, index + 1, word) or  ExistCharacter(i + 1, j, index + 1, word)  

        # unmark the current character  
        board[i][j] = word[index]  
        return found
      if (word == ""): 
          return False   

      # iterate over the board  
      for i in range(len(board)):
          for j in range(len(board[0])):
              if (ExistCharacter(i, j, 0, word)): 
                  return True   

      return False