Hackerrank Absolute Permutation Solution

We define  to be a permutation of the first  natural numbers in the range . Let  denote the value at position  in permutation  using -based indexing.

is considered to be an absolute permutation if  holds true for every .

Given  and , print the lexicographically smallest absolute permutation . If no absolute permutation exists, print -1.

For example, let  giving us an array . If we use  based indexing, create a permutation where every . If , we could rearrange them to :pos[i] i |Difference|3 1 24 2 21 3 22 4 2

Function Description

Complete the absolutePermutation function in the editor below. It should return an integer that represents the smallest lexicographically smallest permutation, or  if there is none.

absolutePermutation has the following parameter(s):

• n: the upper bound of natural numbers to consider, inclusive
• k: the integer difference between each element and its index

Input Format

The first line contains an integer , the number of test cases.
Each of the next  lines contains  space-separated integers,  and .

Constraints

Output Format

On a new line for each test case, print the lexicographically smallest absolute permutation. If no absolute permutation exists, print -1.

Sample Input

3
2 1
3 0
3 2

Sample Output

2 1
1 2 3
-1

Explanation

Test Case 0:

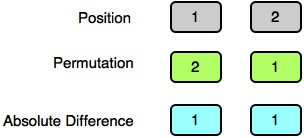
Test Case 1:

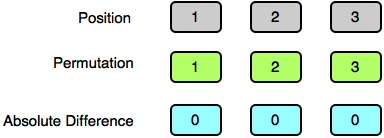
Test Case 2:
No absolute permutation exists, so we print -1 on a new line.

Solution in Python

Sample Input:

1
100 2

Output:

3 4 1 2 7 8 5 6 11 12 9 10 15 16 13 14 19 20 17 18 23 24 21 22 27 28 25 26 31 32 29 30 35 36 33 34 39 40 37 38 43 44 41 42 47 48 45 46 51 52 49 50 55 56 53 54 59 60 57 58 63 64 61 62 67 68 65 66 71 72 69 70 75 76 73 74 79 80 77 78 83 84 81 82 87 88 85 86 91 92 89 90 95 96 93 94 99 100 97 98

The required solution creates a sort of pattern.

Example, k = 2 and n = 60, our answer will follow this pattern

3 4 1 2
7 8 5 6
11 12 9 10 
... upto 60

Example, k = 3 and n = 60, our answer will follow this pattern

4 5 6 1 2 3
10 11 12 7 8 9
16 17 18 13 14 15
... upto 60

From the above two examples we can conclude that n must be divisible by k*2 i.e. n%(k*2) must be 0

Therefore our program will be written to create the above pattern

from itertools import permutations

def absolutePermutation(n, k):
    if k ==0:
    	#When k=0 we just have to print 1 to n 
        print(*(range(1,n+1)))
    elif (n/k)%2!=0.0:
    	#pattern is not possible when k*2 is not divisible by n
        print(-1)
    else:
    	#initialize an empty list
        arr = []
        #create a for loop with k*2 difference, example when k=3 --> 1,7,13,19,25....
        for i in range(1,n,k*2):
        	#numbers from i to i+k*2 example when k=3 and i = 1 --> [1,2,3,4,5,6]
            d = list(range(i, i+k*2)) 
            #Slice and interchange left and right part, example [1,2,3,4,5,6] --> [4,5,6,1,2,3]
            arr+=d[k:]+d[:k]
        print(*arr)

for _ in range(int(input())):
    n,k = map(int,input().split())
    absolutePermutation(n, k)