Hackerrank Even Tree Solution

You are given a tree (a simple connected graph with no cycles).
Find the maximum number of edges you can remove from the tree to get a forest such that each connected component of the forest contains an even number of nodes.
As an example, the following tree with nodes can be cut at most time to create an even forest.
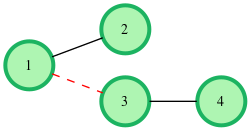
Function Description
Complete the evenForest function in the editor below. It should return an integer as described.
evenForest has the following parameter(s):
- t_nodes: the number of nodes in the tree
- t_edges: the number of undirected edges in the tree
- t_from: start nodes for each edge
- t_to: end nodes for each edge, (Match by index to t_from.)
Input Format.
The first line of input contains two integers and , the number of nodes and edges.
The next lines contain two integers and which specify nodes connected by an edge of the tree. The root of the tree is node .
Constraints.
Note: The tree in the input will be such that it can always be decomposed into components containing an even number of nodes. is the set of positive even integers.
Output Format.
Print the number of removed edges.
Sample Input 1CopyDownload.%0Undirected Graph: t22112--1 333--1444--3555--2666--1777--2888--6999--8101010--8 10 9
2 1
3 1
4 3
5 2
6 1
7 2
8 6
9 8
10 8
Sample Output 1
2Explanation 1
Remove edges and to get the desired result.
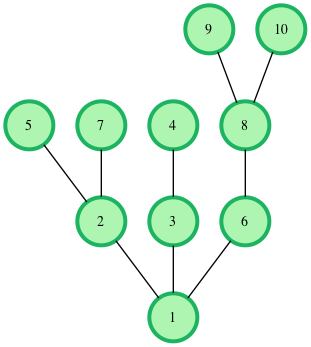
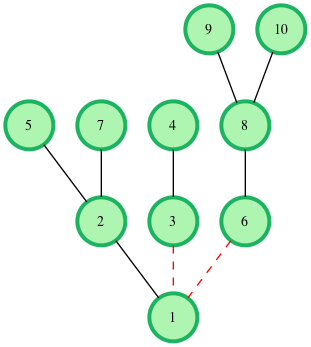
No more edges can be removed.
Solution in java8
Approach 1.
import java.io.*;
import java.util.*;
public class Solution {
public static Map<Integer, ArrayList<Integer>> tree;
public static int count;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int numOfNodes = scanner.nextInt();
int numOfEdges = scanner.nextInt();
tree = new HashMap<Integer, ArrayList<Integer>>();
for (int i = 1; i <= numOfNodes; i++) {
tree.put(i, new ArrayList<Integer>());
}
for (int i = 0; i < numOfEdges; i++) {
int child = scanner.nextInt();
int parent = scanner.nextInt();
ArrayList<Integer> parentNode = tree.get(parent);
parentNode.add(child);
}
for (int i = 2; i <= tree.size(); i++) {
if ((countChildren(i) % 2) != 0) {
count++;
}
}
System.out.println(count);
}
public static int countChildren(int node) {
int totalChild = tree.get(node).size();
for (int child : tree.get(node)) {
totalChild += countChildren(child);
}
return totalChild;
}
}Approach 2.
import java.io.*;
import java.util.*;
public class Solution {
static int n;static boolean b[];static int ar[];
public static void main(String[] args) {
Scanner sc=new Scanner (System.in);
n=sc.nextInt();int e=sc.nextInt();
int a[][]=new int[n][n];
ar=new int[n];int c=0;
for(int i=0;i<e;i++)
{
int x=sc.nextInt()-1,y=sc.nextInt()-1;
a[x][y]++;
a[y][x]++;
}
b=new boolean[n];
b[0]=true;
child(a,0);
for(int i=1;i<n;i++)
if(ar[i]%2==0&&ar[i]!=0)
c++;
System.out.println(c);
}
public static int child(int a[][], int x)
{
int sum=0;
for(int j=0;j<n;j++)
{
if(a[x][j]!=0&&b[j]==false)
{
b[j]=true;
sum+=child(a,j)+1;
}
}
ar[x]=sum+1;
return sum;
}
}Approach 3.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
class Node {
public int val;
public int root;
Node(int r) {
val = 1;
root = r;
}
}
public class EvenTree {
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] inp = br.readLine().split(" ");
int n = Integer.parseInt(inp[0]);
int m = Integer.parseInt(inp[1]);
Node[] nodeArr = new Node[n];
nodeArr[0] = new Node(-1);
for(int i = 1; i < n; i++) {
inp = br.readLine().split(" ");
int u = Integer.parseInt(inp[0]);
int v = Integer.parseInt(inp[1]);
nodeArr[i] = new Node(v-1);
}
for(int i = n-1; i > 0; i--) {
nodeArr[nodeArr[i].root].val += nodeArr[i].val;
}
int count = 0;
for(int i = n-1; i > 0; i--) {
if(nodeArr[i].val % 2 == 0){
count++;
}
}
for(int i = 0; i < n; i++) {
// System.out.println("i => " + i + ", val => " + nodeArr[i].val + ", root => " + nodeArr[i].root);
}
System.out.println(count);
}
}
Solution in python3
Approach 1.
tn, te = map(int, input().rstrip().split())
ch = {}
tr = {}
for i in range(te):
tf, tt = map(int, input().rstrip().split())
if tt not in tr.keys(): tr[tt] = [tf]
else: tr[tt].append(tf)
ch[i] = 1
for i in range(te+1, 1, -1):
if i not in tr.keys():
ch[i] = 1
else:
for j in tr[i]:
ch[i] += ch[j]
c = 0
for i in range(te):
if ch[i] % 2 == 0:
c+=1
print(c)
Approach 2.
class Node:
def __init__(self):
self.parent = None
self.size = 1
#Add parent of child.
def add_parent(self, parent):
# "self" contain child object reference.
#so i assign "parent" object as parent node of child.
self.parent = parent
# Increase size of all above parent.
while parent:
parent.size += 1
parent = parent.parent
if __name__ == '__main__':
t_nodes, t_edges = map(int, input().rstrip().split())
nodes = [Node() for _ in range(t_nodes+1)]
for i in range(t_edges):
t_from, t_to = map(int, input().rstrip().split())
nodes[t_from].add_parent(nodes[t_to])
res = sum(1 for node in nodes[1:] if node.size % 2 == 0 and node.parent is not None)
print(str(res) + '\n')
Approach 3.
#!/bin/python3
import math
import os
import random
import re
import sys
# Complete the evenForest function below.
def evenForest(t_nodes, t_edges, t_from, t_to):
N = t_nodes
E = [[] for _ in range(N)]
for v1, v2 in zip(t_from, t_to):
E[v1-1].append(v2-1)
E[v2-1].append(v1-1)
score = [1] * N
singles = [i for i in range(N) if len(E[i]) == 1]
cuts = 0
while singles:
nd = singles.pop()
if not E[nd]:
continue
neighbour = E[nd][0]
if score[nd] % 2 == 0:
cuts += 1
else:
score[neighbour] += score[nd]
E[neighbour].pop(E[neighbour].index(nd))
if len(E[neighbour]) == 1:
singles.append(neighbour)
return cuts
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t_nodes, t_edges = map(int, input().rstrip().split())
t_from = [0] * t_edges
t_to = [0] * t_edges
for i in range(t_edges):
t_from[i], t_to[i] = map(int, input().rstrip().split())
res = evenForest(t_nodes, t_edges, t_from, t_to)
fptr.write(str(res) + '\n')
fptr.close()
Solution in cpp
Approach 1.
#include<cstdio>
using namespace std;
int n,m,i,j,x,y,k,copii[104],tata[104],v[104],a[104][104];
int nod(int k,int t)
{
for(int i=1;i<=a[k][0];i++)
if(a[k][i]!=t)
copii[k]+=1+nod(a[k][i],k);
tata[k]=t;
return copii[k];
}
int main()
{
//freopen("input","r",stdin);
//freopen("output","w",stdout);
scanf("%d %d",&n,&m);
for(i=1;i<=m;i++)
{
scanf("%d %d",&x,&y);
a[x][0]++;
a[y][0]++;
a[x][a[x][0]]=y;
a[y][a[y][0]]=x;
}
copii[1]=nod(1,0);
for(i=1;i<=n;i++)
{
if(copii[i]%2==1&&tata[i]!=0)
{
tata[i]=0;
k++;
}
}
printf("%d",k);
return 0;
}
Approach 2.
#include <cmath>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
int t;
void dfs(vector<vector<int> >& ver, vector<int>& first, vector<int> &last, int root)
{
first[root] = t;
++t;
for(int i = 0; i < ver[root].size(); ++i){
if(first[ver[root][i]] == -1)
dfs(ver, first, last, ver[root][i]);
}
last[root] = t;
}
int main() {
int v, e;
cin >> v >> e;
vector<vector<int> > ver(v);
int start, end;
for(int i = 0; i < e; ++i)
{
cin >> start >> end;
ver[start - 1].push_back(end - 1);
ver[end - 1].push_back(start - 1);
}
vector<int> first(v, -1);
vector<int> last(v, -1);
t = 0;
dfs(ver, first, last, 0);
int res = 0;
for(int i = 0; i < v; ++i)
if((last[i] - first[i])%2 == 0)
++res;
cout<<res-1<<endl;
}
Approach 3.
#include <cmath>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
#include <ios>
#include <cstring>
using namespace std;
vector<int> graph[100];
bool visited[100];
int ans;
int dfs(int node) {
visited[node] = true;
int num_vertex = 0;
for(unsigned int i = 0; i < graph[node].size(); i++) {
int v = graph[node][i];
if(!visited[v]) {
int num_nodes = dfs(v);
if(num_nodes & 1)
num_vertex += num_nodes;
else
ans++;
}
}
return num_vertex + 1;
}
int main() {
ios_base::sync_with_stdio(false);
int m, n;
cin >> n >> m;
int u, v;
for(int i = 0; i < m; i++) {
cin >> u >> v;
graph[u - 1].push_back(v - 1);
graph[v - 1].push_back(u - 1);
}
ans = 0;
memset(visited, false, sizeof(bool) * 100);
dfs(0);
cout << ans << endl;
return 0;
}
