Hackerrank - Strange Counter Solution

Bob has a strange counter. At the first second, it displays the number . Each second, the number displayed by the counter decrements by  until it reaches .

The counter counts down in cycles. In next second, the timer resets to  and continues counting down. The diagram below shows the counter values for each time  in the first three cycles:

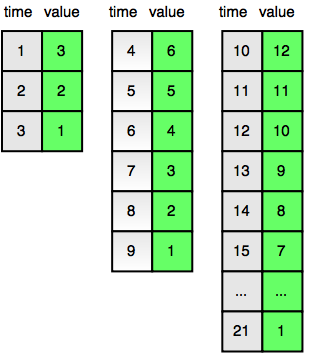
Find and print the value displayed by the counter at time .

Function Description

Complete the strangeCounter function in the editor below. It should return the integer value displayed by the counter at time .

strangeCounter has the following parameter(s):

• t: an integer

Input Format

A single integer denoting the value of .

Constraints

Subtask

• for  of the maximum score.

Output Format

Print the value displayed by the strange counter at the given time .

Sample Input

4

Sample Output

6

Explanation

Time  marks the beginning of the second cycle. It is double the number displayed at the beginning of the first cycle:. This is also shown in the diagram in the Problem Statement above.

Solution in Python

def strangeCounter(t):
    n=3
    while 2*n-2<=t:
        n*=2
    return n-(t-(n-2))

print(strangeCounter(int(input())))

Answer explanation

We can see that the number on the top right corner of each cycle equals to the 3rd item on the left column. And also it equals to the number of rows in that particular cycle.

Another interesting pattern we can observe is that the number on the top right corner doubles each cycle 3, 6, 12, 24, 48.....

We can use this value to check in which cycle our given time falls.

Let us assume t = 15

First we will find in which cycle 15 falls in. Let us start by initializing n = 3

For n=3, the values of t will range from n-2 =1 to n-2+n=4 (4 exclusive), n-2+n can also be written as n*2-2.

Now, since t = 15 doesn't fall between 1 and 3 we will double the value of n.

For n = 6, t ranges from n-2=4 to n-2+n=10.

Again, t = 15 doesn't fall under 6 and 10. Therefore we will double the value of n again.

For n = 12, t ranges from n-2 = 10 to n-2+n = 22.

t = 15 falls between 10 to 22.

Now we subtract the starting number of our cycle which is n-2=10 from t.

t-(n-2) = 15-10=5

Now we just have to subtract the result from n and we will get our required answer

n-5  = 12-5  = 7